Wave plate

A wave plate or retarder is an optical device that alters the polarization state of a light wave travelling through it.

Operation

A wave plate works by shifting the phase between two perpendicular polarization components of the light wave. A typical wave plate is simply a birefringent crystal with a carefully chosen orientation and thickness. The crystal is cut so that the extraordinary axis or "optic axis" is parallel to the surfaces of the plate. Light polarized along this axis travels through the crystal at a different speed than light with the perpendicular polarization, creating a phase difference. When the extraordinary index is smaller than the ordinary index, as in calcite, the extraordinary axis is called the "fast axis" and the perpendicular direction in the plane of the surfaces is called the "slow axis".

Depending on the thickness of the crystal, light with polarization components along both axes will emerge in a different polarization state. The wave plate is characterized by the amount of relative phase, \Gamma, that it imparts on the two components, which is related to the birefringence Δn and the thickness L of the crystal by the formula

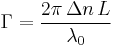
\Gamma = \frac{2 \pi\, \Delta n\, L}{\lambda_0}

where 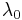\lambda_0 is the vacuum wavelength of the light. For instance a quarter-wave plate creates a quarter-wavelength phase shift and can change linearly polarized light to circular and vice versa. This is done by adjusting the direction of the linear polarization of the incident light so that it makes 45° angle with the fast axis. This gives ordinary and extraordinary waves with equal amplitude.

The other common type of wave plate is a half-wave plate, which retards one polarization by half a wavelength, or 180 degrees. This type of wave plate changes the polarization direction of linear polarized light. Wave plates in general as well as polarizers can be described using the Jones matrix formalism, which uses a vector to represent the polarization state of light and a matrix to represent the linear transformation of a wave plate or polarizer.

Although the birefringence Δn may vary slightly due to dispersion, this is negligible compared to the variation in phase difference according to the wavelength of the light due to the fixed path difference (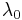\lambda_0 in the denominator in the above equation). Waveplates are thus manufactured to work for a particular range of wavelengths. The phase variation can be minimized by stacking two waveplates that differ by a tiny amount in thickness back-to-back, with the slow axis of one along the fast axis of the other. With this configuration, the relative phase imparted can be, for the case of a quarter-wave plate, one-fourth a wavelength rather than three-fourths or one-fourth plus an integer. This is called a zero-order wave plate.

For a single wave plate changing the wavelength of the light introduces a linear error in the phase. Tilt of the wave plate enters via 1/cos into the path length and thus only quadratically into the phase. For the extraordinary polarization the tilt also changes the refractive index to the ordinary via cos, so combined with the path length, the phase shift for the extraordinary light due to tilt is zero.

A polarization independent phase shift of zero order needs a plate with thickness of one wavelength. For Calcite the refractive index changes in the first decimal place, so that a true zero order plate is ten times as thick as one wavelength. For quartz and magnesium fluoride the refractive index changes in the second decimal place and true zero order plates are common for wave-lengths above 1 µm.

See also

External links